Окружности, длины радиусов которых равны 2 см и 4 см внешним образом касаются в точке О....

Question

Окружности, длины радиусов которых равны 2 см и 4 см внешним образом касаются в точке О. Общая касательная двух окружностей проходит через точку О и пересекает другую общую касательную в точке Р. Вычислите расстояние между точками О и Р.

Answer 1

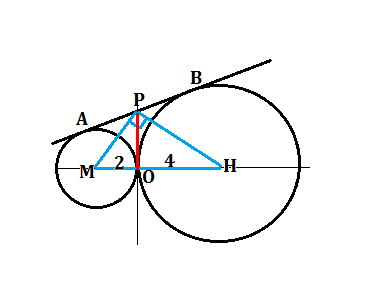
Пусть центры окружностей будут М и Н, точки касания их со второй касательной А и В. 
Центр окружности М лежит на биссектрисе угла АРО, центр окружности Н лежит на биссектрисе угла ВРО. 
Т.к. угол АРВ-  развернутый и равен 180º, угол МРН=180º:2=90º.
В прямоугольном треугольнике МРН высота есть среднее геометрическое между отрезками гипотенузы, на которые она делится высотой. 
РО=√(МО*ОН)=√2*4=2√2

---