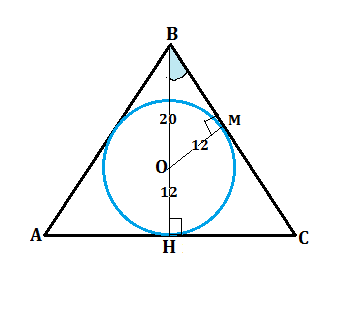Проведем из вершины В высоту ВН к АС. В равнобедренном треугольнике высота еще биссектриса и медиана. ⇒ АН=НС
ВО=20 см, ОН=12 см.
ВН=ВО+ОН=32 см
Из центра вписанной окружности проведем радиус ОМ в точку касания с боковой стороной ВС.
∠ВМО=90º ( радиус в точке касания перпендикулярен стороне),
ОМ=12 см
ВМ =16 ( не делала вычислений, т.к. прямоугольный треугольник с отношением катета и гипотенузы 3:5- египетский. Можно найти ВМ и по т. Пифагора)
Треугольники ВНС и ВМО подобны: прямоугольные и имеют общий угол В.
Тогда ВО:ВС=ВМ:ВН
20:ВС=16:32
16 ВС=640
ВС-40 см
Отрезки касательных из одной точки до точки касания равны.
⇒ МС=НС
МС=ВС-МС= 40-16=24 см
АС=2НС=24*2=48 см
Р=АВ+ВС+АС=40+40+48=128 см