длины сторон прямоугольника равны 8 и 6 см через точку О пересечения его диагоналей...

Question

длины сторон прямоугольника равны 8 и 6 см через точку О пересечения его диагоналей проведена прямая ОК перпендикулярная его плоскости найдите расстояние от точки К до вершины прямоугольника если ОК=12 --------------//-------/-/-/-// 2 задача. длины сторон прямоугольника ABC соответственно равны ВС=15 АВ=13 АС=4. через сторону АС проведена плоскость альфа состовляющая с плоск. данного треуг. угол 30°. найти расстояние от вершины В до плоскости альфа. геометрия 10 класс

Answer 1

2)

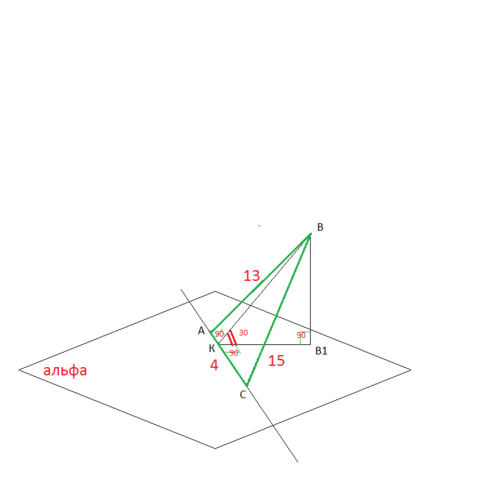
Сделаем построение  по условию.

Прямая АС линия пересечения плоскости АЛЬФА и плоскости треугольника (АВС).

Построим проекцию т.В  на плоскость АЛЬФА - т.В1

ВВ1 - перпендикуляр  к плоскости АЛЬФА.

Отрезок  ВВ1 – это расстояние от вершины  В  до плоскости  АЛЬФА.

Опустим перпендикуляр из вершины В на основание АС в точку  К.

ВК– это наклонная, тогда отрезок В1К – это проекция ВК.

По теореме о трех перпендикулярах – треугольник ВКВ1 – прямоугольный.

Найдем высоту  BK  в ∆АВС .

Периметр ∆АВС  Р=АВ+ВС+АС=13+15+4=32

Полупериметр р=Р/2=22/2=16

По формуле Герона площадь треугольника  

S∆= √p(p-AB)(p-BC)(p-AC)= √16*(16-13)(16-15)(16-4)=24

Еще одна формула для площади  S=1/2*ВК*АС

BK = 2S /AC = 2*24/4= 12

Тогда в прямоугольном треугольнике ∆ВКВ1:  ВВ1 = ВК*sin30=12*1/2 =6

ОТВЕТ   6

 

---