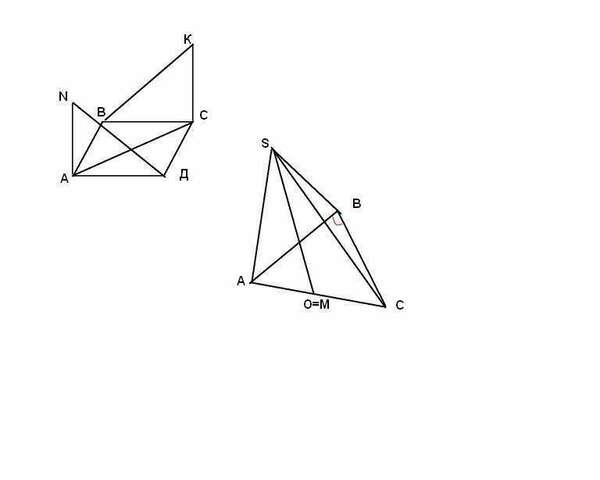
1) параллелограмм АВСД: АВ||СД, ВС||АД
AN⊥ABC и KC⊥AВC
Т.к. если прямая перпендикулярна к плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости (AN⊥AC и КС⊥АС)
Плоскость КВС⊥плоскости АВС, т.к. плоскость КВС проходит через прямую КС, перпендикулярную к АВС (согласно теореме: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны).
Аналогично плоскость ANД⊥плоскости АВС, т.к. плоскость ANД проходит через прямую AN, перпендикулярную к АВС.
Т.к. плоскости ANД и КВС, перпендикулярные к одной прямой АС, значит они параллельны.
2) Прямоугольный ΔАВС (∠В прямой)
Из точки S опустим перпендикуляр SO на плоскость АВС.
По условию точка S равноудалена от вершин прямоугольного треугольника и не лежит в плоскости этого треугольника, значит наклонные SA=SB=SC , а следовательно и их проекции на плоскость АВС ОА=ОВ=ОС. Значит О - центр описанной окружности около ΔАВС.
Т.к. в прямоугольном треугольнике центром описанной окружности является середина гипотенузы М, то значит точки О и М совпадают, тогда SM перпендикулярна плоскости АВС