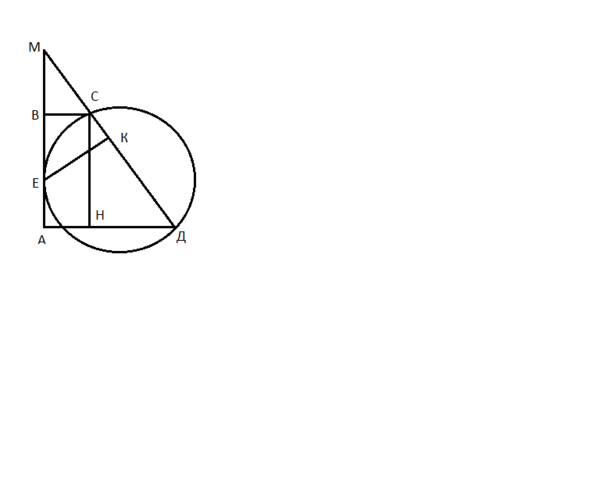В прямоугольной трапеции АВСД АД||ВС, значит <ДАВ=<АВС=90°.<br>Расстояние от Е до СД - это перпендикуляр ЕК к СД.
Из вершины С опустим высоту СН на АД: АВ=СН, ВС=АН=12
АД=АН+НД
НД=АД-АН=14-12=2.
Продолжим стороны АВ и СД до пересечения в точке М.
Прямоугольные ΔМВС и ΔСНД подобны по острому углу (<ВСМ=<НДС как соответственные углы при пересечении параллельных прямых АД и ВС секущей МД)<br>ВС/НД=МС/СД
12/2=МС/СД
МС=6СД
МД=МС+СД=6СД+СД=7СД
Получается, что МЕ - касательная и МД - секущая, проведённые к окружности из одной точки.
Значит МЕ²=МД*МС=7СД*6СД=42СД²
МЕ=СД√42
Прямоугольные ΔМКЕ и ΔСНД подобны по острому углу (<ЕМК=<ДСН как соответственные углы при пересечении параллельных прямых АМ и СН секущей МД)<br>МЕ/СД=ЕК/НД
СД√42/СД=ЕК/2
ЕК=2√42