Рисунки ко всем задачам прикреплены и пронумерованы.
№ 1.
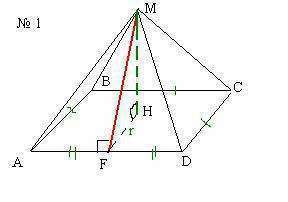
Дано: MABCD - правильная 4-угольная пирамида
ABCD - квадрат
AB=6 см., MF=4 см - апофема пирамиды
MH - высота пирамиды.
Найти: а) MD - ?
б) MH - ?
в) Sпол - ?
Решение:
а) т.к. MF - апофема пирамиды, то MF⊥AD, ΔAMD - равнобедренный (AM=MD) => MF - высота, медиана и биссектриса, значит AF=FD=3 см.
ΔMFD - прямоугольный, по теореме Пифагора: MD=√(MF²+FD²)=√(4²+3²)=5 см.
б) ΔMFH - прямоугольный (MH⊥FH) => по теореме Пифагора: MH=√(MF²-FH²)
FH - радиус вписанной в квадрат окружности, равен половине стороны квадрата, FH=3 см.
MH=√(MF²-FH²)=√(4²-3²)=√7 см.
в) Sпол= Sосн+Sбок
Sбок=0.5*Pосн*MF=0.5*(6*4)*4=48 см²
Sосн=6*6=36 см²
Sпол=48+36=84 см²
№ 2.
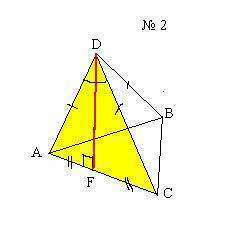
Дано: DABC - правильная треугольная пирамида
Sосн=4√3 дм²
Sпол=16√3 дм²
Найти: 1) DC - ?
2) плоский угол при вершине D=∠ADC - ?
Решение: 1) Sбок=Sпол-Sосн=16√3-4√3=12√3 дм²
Sбок=0.5*Pосн*DF
по формуле Герона: Sосн=√p(p-AC)³=(p-AC)*√p(p-AC)
p=P/2=3AC/2 - полупериметр основания
Sосн=


 дм.
дм.
Pосн=3AC=3*4=12 дм.
Sбок=0.5*Pосн*DF=0.5*12*DF=12√3
DF=2√3 дм.
ΔFDC - прямоугольный, по теореме Пифагора: DC=√(DF²+FC²)=√(12+4)=4 дм.
2) ΔFDC - прямоугольный, по определению синуса:
sin(∠ADC)=FC/DC=2/4=1/2 => ∠ADC=30°
№ 3.
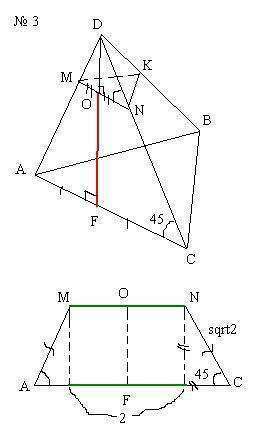
Дано: MKNABC - усеченная правильная пирамида
ABC - большее основание, MNK - меньшее основание
MN=2 см.
NC=√2 см.
∠ACN=45°
Найти: 1) Sбок.ус - ?
2) Sбок.ус/Sбок - ?
Решение:
1) Sбок.ус = 0.5*(P1+P2)*OF
OF - апофема усеченной пирамиды
P1=Pabc
P2=Pmnf=3*2=6 см.
Рассмотрим трапецию MNCA - равнобедренная (AM=NC) => OF=1 см.
(т.к. OF является высотой трапеции).
AC=1+2+1=4 см. (см. рисунок)
P1=3*4=12 см.
Sбок.ус = 0.5*(12+6)*1=0.5*18=9 см²
2) Sбок=0.5*P1*DF=0.5*12*DF=6DF
В ΔMDN - равнобедренный: ON=OM=1 см.
∠DNO=∠NCA=45° (как соответственные углы при параллельных прямых MN и AC и секущей DC) => ON=DO=1 см.
DF=DO+OF=1+1=2 см.
Sбок=6DF=6*2=12 см²
Sбок.ус/Sбок=9/12=3/4=0.75=75%