В треугольнике АВС ВС продолжена за точку С. Проведены Биссектрисы углов АСД и АВС....

Question

В треугольнике АВС ВС продолжена за точку С. Проведены Биссектрисы углов АСД и АВС. Доказать, что угол Е образовавшийся при пересечении биссектрис, равен половине угла А

Answer 1

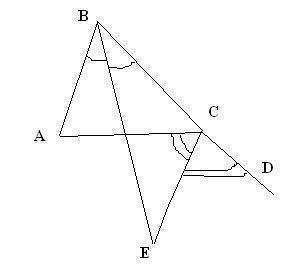
1) Рассмотрим ΔABC:
∠BAC+∠ABC+∠BCA=180°
т.к. ∠ABC=2∠EBC, то:
∠BAC+2∠EBC+∠BCA=180°
2) Рассмотрим ΔBEC:
∠EBC+(90°-0.5∠BCA)+∠BCA+∠BEC=180°
т.к. ∠ACE=(180°-∠BCA)/2
∠EBC+0.5∠BCA+∠BEC=90°
3) Из п. 1 следует:
∠BAC=180°-2∠EBC-∠BCA
Из п. 2 следует:
∠BEC=90°-∠EBC-0.5∠BCA
4) Домножим второе уравнение из п.3 на 2:
2∠BEC=180°-2∠EBC-∠BCA, что равно ∠BAC. Следовательно:
∠BAC=2∠BEC или ∠BEC=0.5∠BAC

---