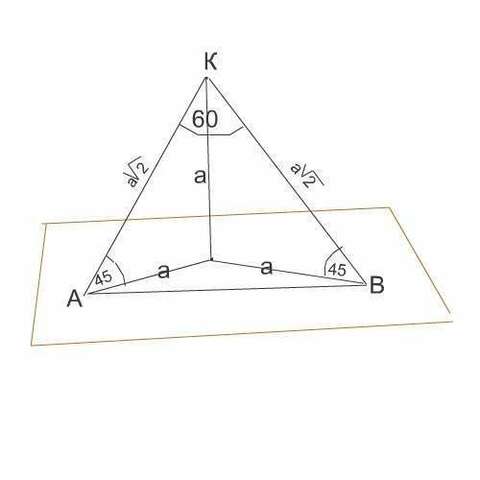
Сделаем рисунок.
Обозначим точку вне плоскости К,
основание перпендикуляра, соединяющего эту точку с плоскостью, обозначим О,
концы наклонных на плоскости А и В.
Так как наклонные с плоскостью образуют угол 45º, а расстояние от К до плоскости перпендикуляр, треугольник АКО и ВКО равнобедренные прямоугольные, проекциинаклонных равны расстоянию от К до плоскости и равныа.
Следовательно, наклонные равны между собой, т.к. их проекции равны.
Найдем их длину.
Она равна диагонали квадрата со сторонами, равными катетам равнобедренного прямоугольного треугольника и находится по формуле:
d=а√2
АК=КВ=а√2
Теперь соединим А и В и рассмотрим образовавшийся треугольник АКВ.
Он образован равными боковыми сторонами АК и КВ,
а так как угол между наклонными равен 60º, треугольник этот не просто равнобедренный, а равносторонний.
Следовательно, АВ - расстояние между концами наклонных- равно а√2.