3) Раскроем модуль и найдём критические точки.
Получаем 2 квадратных уравнения:
x² - 5x - 6 = 0 (1)
x² + 5x -6 = 0 (2)
Решаем (1):
x² - 5x - 6 = 0
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-5)^2-4*1*(-6)=25-4*(-6)=25-(-4*6)=25-(-24)=25+24=49;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√49-(-5))/(2*1)=(7-(-5))/2=(7+5)/2=12/2=6;
x₂=(-√49-(-5))/(2*1)=(-7-(-5))/2=(-7+5)/2=-2/2=-1.
Решаем (2):
x² + 5x - 6 = 0
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=5^2-4*1*(-6)=25-4*(-6)=25-(-4*6)=25-(-24)=25+24=49;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√49-5)/(2*1)=(7-5)/2=2/2=1;
x₂=(-√49-5)/(2*1)=(-7-5)/2=-12/2=-6.
Совмещая оба решения, находим значения функции больше нуля: -6 > x > 6.
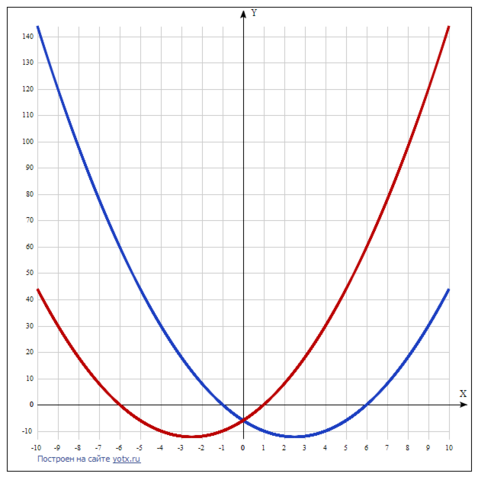
Графически положительные значения параболы находятся выше оси х начиная от тех значений, где парабола пересекает ось х и переходит в вехнюю половину графика.
В приложении даются графики обеих функций.