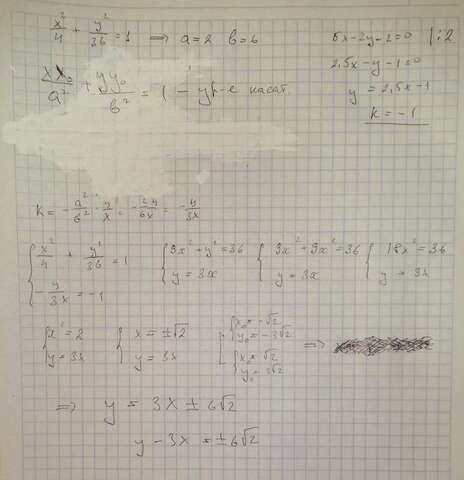Раз касательная параллельная исходной прямой, значит, у них совпадает коэффициент k. Находишь его, а затем и коэффициент k для касательной. Приравниваешь их. Затем пишешь систему с двумя неизвестными для уравнения эллипса и уравнения касательной. Решаешь.
Полученные значения  подставляешь в уравнение касательной и получаешь два уравнения. Это потому что касательных к эллипсу две. Мяк
подставляешь в уравнение касательной и получаешь два уравнения. Это потому что касательных к эллипсу две. Мяк