1. Область определения: 
2. МНожество значений: 
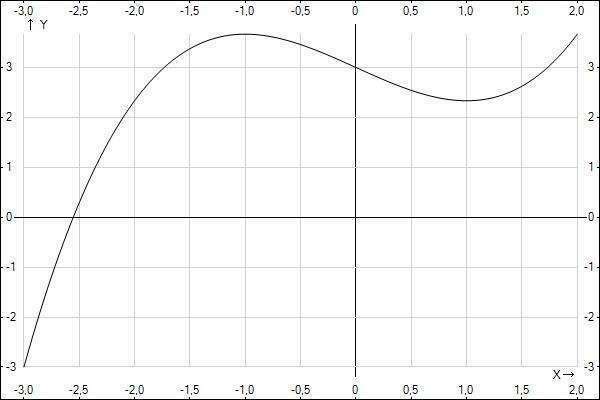
3. Найдем точки экстремума:
Находим производную:

Приравниваем ее к нулю:



Найденные точки разбивают область определения на три интервала:

Найдем знаки производной в этих интервалах, подставив значения из них (-2; 0; 2):
+ - +
Это значит, что функция на первом и последнем промежутках возрастает, а на среднем - убывает.
/ \ /
Найдем начения функции в этих точках:
1/3*(-1)^3-(-1)+3=-1/3+1+3=4-1/3=3+2/3=3,6666666
1/3*(1)^3-(1)+3=1/3-1+3=2+1/3=2+1/3=2,33333333
Т.о. функция вначале возрастает на промежутке  от
от  до
до  , после этого убывает на промежутке
, после этого убывает на промежутке  до
до  , и затем снова возрастает на промежутке
, и затем снова возрастает на промежутке  до
до 
Осталось найти точки пересечения с осями координат:
ПРи х=0 у=3