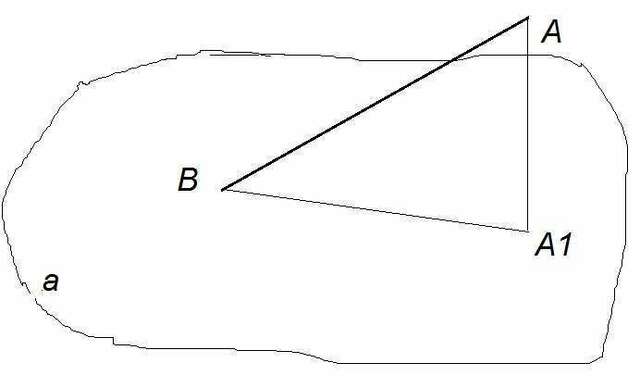
Смотрите рисунок.
Прямая АВ, перпендикуляр АА1 на плоскость "а" и проекция на
плоскость прямой АВ образуют прямоугольный треугольник с углом АВА1 = 30
градусов и прямым углом АА1В. В прямоугольном треугольнике против угла 30
градусов лежит катет равный половине гипотенузы. Следовательно,
1) АА1= АВ/2 = 24/2 = 12 см. Из теоремы
Пифагора (ВА1)²= (АВ)² – (АА1)² = 24² – 12² = 576 – 144 = 432. Отсюда ВА1 = √432 = 12√3
Если
АА1 обозначить Х, то АВ = 2Х. Тогда в общем виде квадрат длины проекции (ВА1)² = (2Х)² – X²=3Х²,
а ВА1 = Х√3. Таким образом, можно
сразу записать, что
2) ВА1 = 8√3. А вспомнив, что катет
против 30 градусов равен половине гипотенузы, имеем АВ = АА1*2 = 8*2 = 16 см
3) Квадрат ВА1 = 15² = 225. И это равно
3Х². Т.е. 225 = 3Х². Отсюда Х²=225/3
= 75. Тогда Х = √75 = 5√3. За Х мы приняли АА1. Значит АА1 = Х =
5√3. Тогда АВ = 2Х= 2*5√3 = 10√3