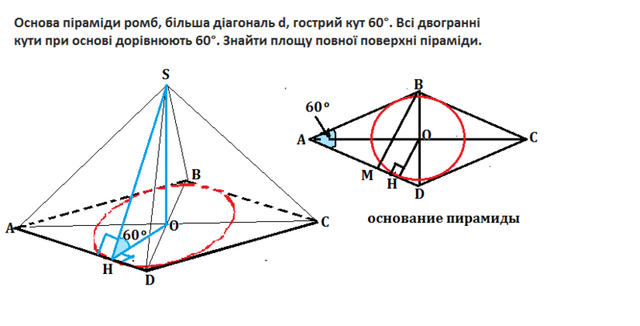
Основание пирамиды - ромб. Большая диагональ d, острый угол =60°. Все двугранные углы при основании равны 60°. Найти площадь полной поверхности пирамиды.
Двугранные углы при основании равны 60°, значит,
проекции апофем равны между собой и
равны радиусу вписанной в данный ромб окружности.
Сделаем рисунок пирамиды
SABCD и отдельно ее основания АВСD.
АС=d
АО=d/2
Сумма углов при стороне параллелограмма равна 180°⇒
∠ABC=180°-60°=120°
∠ABO=120°:2=60°
сторона ромба АВ=АО:sin 60°=
d/√3
∠ОАВ=ОАD=60°:2=30°
ОН=АО:2=d/4 (противолежит углу 30°)
Апофема
SH=OH/cos∠OHS= (d/4):cos60°=(d/4)
:1/2=
d/2=0,5d
Площадь полной поверхности пирамиды равна сумме площадей ее четырех боковых граней и основания.
S ASD=AD*SH
:2=
[0,5d*d/√3];2=0,25d²/√3
Площадь боковой поверхности
Ѕбок=
4*0,25d²/√3=d²/√3
Площадь основания=площадь ромба
Треугольник АВD- равносторонний.
Высота ромба ВМ=АО=d/2
S ABCD=AD*ВМ=(d²/√3):2
Sполн==(d²/√3):2+
d²/√3=3d²/2√3=
(d²√3):2