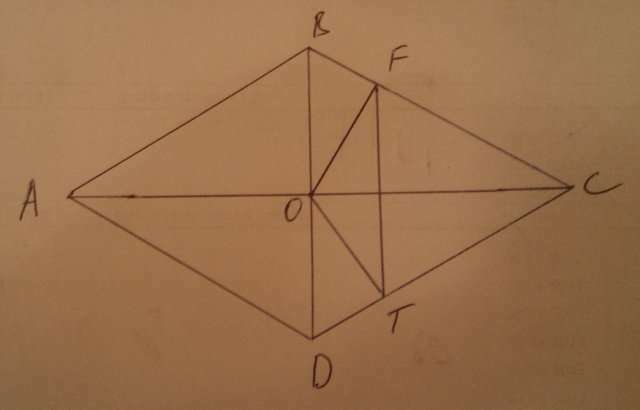
Итак, раз в условии сказано что BD равна стороне DA значит треугольник DВС равносторонний (у ромба все стороны равны). У равностороннего треугольника все углы равны 60 градусам, слудовательно угол СВD = 60 градусам. Поскольку треугольник ОFВ прямоугольный (ОF перпендткуляр к ВС), то значит угол FОВ = 180-90-60=30 градусов. Поскольку угол ВОС прямой, то угол FОС = 90-30 = 60 градусов. Т.к. угол ТОС = FОС, то угол FОТ = 2 * FОС = 2*60=120 градусов.
Если ОF и ОТ перпендикуляры (по условию задачи), значит они равны, следовательно треугольник FОТ - равносторонний. У равностороннего треугольника углы у основания равны. Значит угол ОFТ= углу ОТF и равен (180-120)/2=30 градусов.
Ответ FОТ = 120 градусов, ОFТ= ОТF = 30 градусов