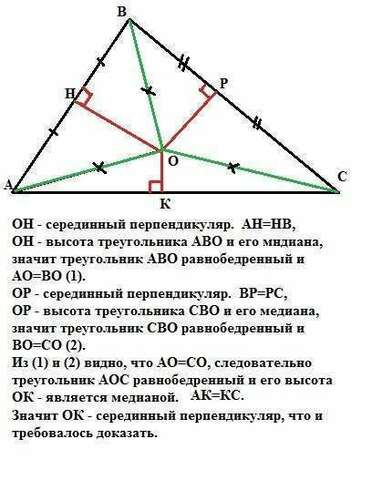
Пусть дан треугольник АВС.
ОН - серединный перпендикуляр к стороне АВ. АН=НВ,
ОН - высота треугольника АВО и его медиана, значит треугольник АВО равнобедренный и АО=ВО (1).
ОР - серединный перпендикуляр к стороне ВС. ВР=РС,
ОР - высота треугольника СВО и его медиана, значит треугольник СВО равнобедренный в ВО=СО (2).
Из (1) и (2) видно, что АО=СО, следовательно треугольник АОС равнобедренный в его высота ОК - является медианой. АК=КС.
Значит ОК - серединный перпендикуляр, что и требовалось доказать.