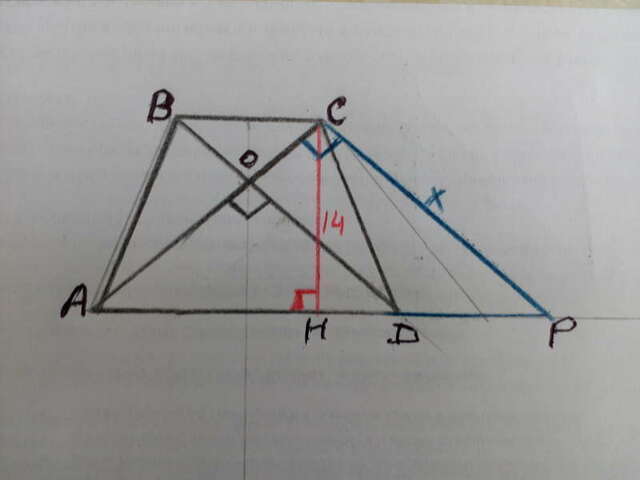
Трапеция АВСD равнобедренная, значит ее диагонали равны. АС=BD.
Проведем прямую СР параллельно диагонали BD до пересечения с продолжением основания AD в точке Р. BCPD параллелограмм и DP=BC.
Треугольник АСР прямоугольный и равнобедренный, так как катеты CP и АС перпендикулярны (АС перпендикулярна BD - дано, а CP параллельна BD по построению).
Пусть катеты AC и CР равны X. Тогда гипотенуза AP=Х√2 (по Пифагору).
CH - высота треугольника АСР, проведенная из вершины прямого угла и равна произведению катетов, деленному на гипотенузу (свойство).
Итак, CH=AC*CP/AP. CH=14см (дано). Тогда
14=Х^2/(Х√2). Отсюда Х=14√2, а АР=14√2*√2=28см.
Но АР=AD+BC. Тогда площадь трапеции равныS=(AD+BC)*CH/2 или S=28*14/2=196 см^2.
Ответ: S=196 см^2.