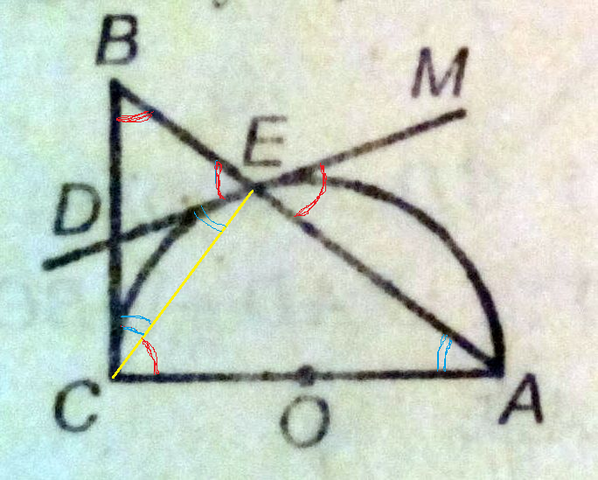
∠ МЕА = половине дуги ЕА - угол между касательной и хордой
∠ЕСА= половине дуги ЕА, как вписанный угол, опирающийся на эту дугу
∠МЕА=∠ЕСА
∠ВЕD=∠МЕА как вертикальные
∠ DЕC = половине дуги CЕ - угол между касательной и хордой
∠ DCT = половине дуги CЕ - угол между касательной и хордой
∠ВАС = половине дуги СЕ, как вписанный угол, опирающийся на эту дугу
∠СBA+∠BAC=90° - сумма острых углов прямоугольного треугольника
∠ВСЕ+∠ЕСА=90°- по условию угол С - прямой
В этих равенствах ∠ВАС=∠ВСЕ
Значит
∠СВА=∠ЕСА, а ∠ЕСА=∠МЕА=∠ВЕD
Итак
∠СВА=∠ВЕD
Треугольник ВDE - равнобедренный