Хорошее условие, я даже сканер пошел присоединять :)))
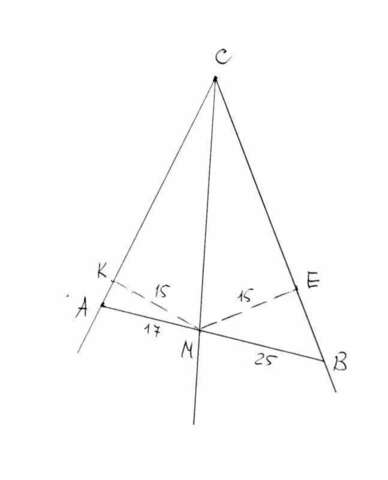
Ясно, что СМ - биссектриса угла АСВ.
Далее, АМ = 17, ВМ = 25 (это легко проверить, АВ = 42).
МК и МЕ - перпендикуляры из точки М на стороны угла АСВ, по условию МК = МЕ = 15.
Если внимательно посмотреть на треугольники АКМ и ЕВМ, то это - Пифагоровы треугольники (это - необязательно, АК и ЕВ можно вычислить просто по теореме Пифагора, просто так ошибиться труднее :)) со сторонами 8, 15, 17 и 15, 20, 25.
То есть АК = 8, ВЕ = 20.
Пусть СК = СЕ = х, тогда АС = х + 8, ВС = х + 20.
По свойству биссектрисы АС/ВС = 17/25
(х + 8)/(х + 20) = 17/25;
25*x + 200 = 17*x + 340;
8*x = 140; x = 35/2;
Площадь АВС проще всего сосчитать так - сумма площадей АКМ, МЕВ и двух одинаковых треугольников МКС и МЕС.
S = 8*15/2 + 20*15/2 + (35/2)*15 = 60+150 + 262,5 = 472,5