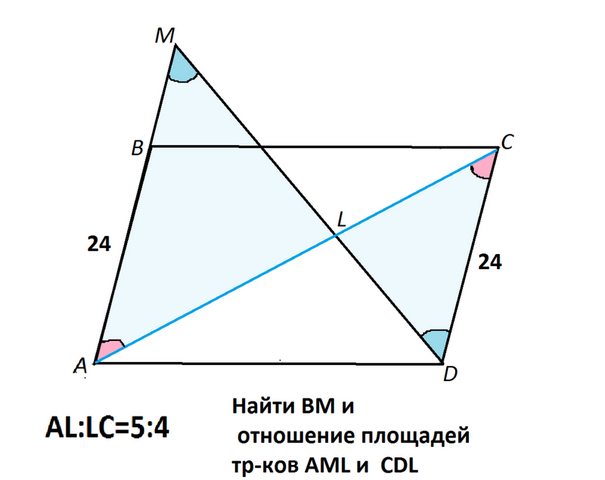
В параллелограмме ABCD проведена диагональ АС.
Через вершину D и точку L, принадлежащую диагонали AC и такую, что AL : LC = 5:4, проведена прямая до пересечения с прямой AB в точке M.
Найти длину BM и
отношение площадейтреугольников AML и CDL если AB= 24 см
Решение:
Четырехугольник
АВСD -параллелограмм.
Следовательно, СD=АВ=24 см
МD - секущая при параллельных АМ и СD.
АС - секущая ири параллельных АМ и СD.
⇒ угол АМD=СDМ, угол АСD=САМ, углы при L в этих треугольниках равны как вертикальные.
⇒ треугольники АМL и СDL подобны с коэффициентом подобия
АL:LС=5:4
⇒АМ:СD=5:4
Произведение средних членов пропорции равно произведению крайних.
4 АМ=5 СD
4 АМ=24*5=120 см
АМ=30 см
ВМ=АМ-АВ=30-24=
6 см
Площади треугольников AML и CDL относятся как квадрат коэффициента их подобия,
т.е. как (5/4)²=25/16