Пожалуйста, помогите решить 2 задачи по геометрии желательно с рисунками и объяснениями

Question

Пожалуйста, помогите решить 2 задачи по геометрии желательно с рисунками и объяснениями

---

Comments

Перепишите решение

Answer 1

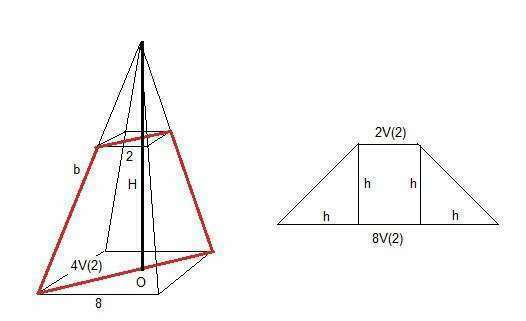
1) Построим осевое сечение этой пирамиды через диагонали оснований.
Получится равнобочная трапеция с углом 45 градусов.
Проводим две высоты h, делим нижнее основание на 3 части:
Поскольку угол 45 градусов, то боковые части равны высоте h,
там получаются прямоугольные равнобедренные треугольники.
8√2 = 2√2 + 2h
h = 6√2/2 = 3√2 - высота усеченной пирамиды.
Опять-таки, поскольку угол наклона ребра равен 45 градусов, высота полной пирамиды H равна половине диагонали основания, H = 4√2.
Длина бокового ребра полно пирамиды по теореме Пифагора
b^2 = (4√2)^2 + (4√2)^2 = 16*2 + 16*2 = 64
b = 8
Значит, боковая поверхность полной пирамиды - это 4 равносторонних треугольника.
S(бок) = 4*S(тр) = 4*8^2*√3/4 = 8^2*√3 = 64√3 - площадь боковой поверхности

---

Comments

не поняла откуда вот это 8√2 = 2√2 + 2h

---

т.е как нашли диагонали оснований?

---

тут опять воображение помогает :) если достроить до полной пирамиды, то это четырехугольная пирамида с квадратом 8х8 в основании. ещё про неё можно сказать, что сечение через вершину пирамиды и диагональ основания - это равнобедренный треугольник с углами при основании 45 градусов, то есть прямоугольный. То есть 1) высота полной пирамиды равна половине диагонали основания, то есть 4√2 2) боковые ребра равны сторонам основания, то есть все боковые грани - равносторонние треугольники.

---

ясно, что высота усеченной пирамиды равна 4√2 - √2 = 3√2; боковая поверхность полной пирамида тоже считается легко - это площадь 4 равносторонних треугольников со стороной 8.

---

диагонали оснований находятся, как обычно находится диагональ квадрата :) сторона, умноженная на √2;