A перпендикулярно (ABC) AB=14 AC=15 CB=13 CM=5 найти: MD=?

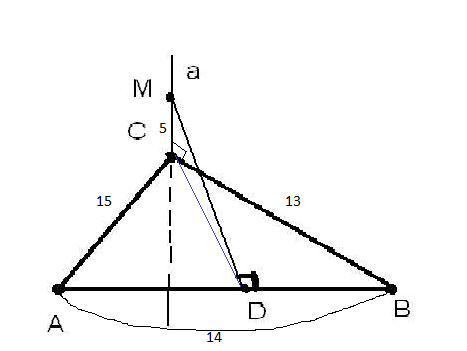
MC⊥ пл (АВС) ⇒ МС перпендикулярна любой прямой, лежащей в этой плоскости, в том числе МС⊥ АВ
MD⊥ AB
Значит, AB перпендикулярна двум пересекающимся прямым плоскости (MCD), поэтому АВ ⊥ плоскости (МСD)
Значит АВ -перпендикуляр к любой прямой этой плоскости, в том числе и к прямой CD.
(по теореме о трех перпендикулярах СD)⊥ AB
CD - высота треугольника АВС

Найдем площадь треугольника АВС по формуле Герона
р= (АВ+ВС+АС)/2=(14+13+15)/2=21

$S= \sqrt{21(21-14)(21-15)(21-13)}= \sqrt{21\cdot 7\cdot 6\cdot 8}=3\cdot 4\cdot 7=84$

C другой стороны,

S=AB·CD/2

84=14·CD/2

CD=12

Из прямоугольного треугольника MCD по теореме Пифагора

MD²=MC²+CD²

MD²=5²+12²

MD²=25+144

MD²=169

MD=13 cм