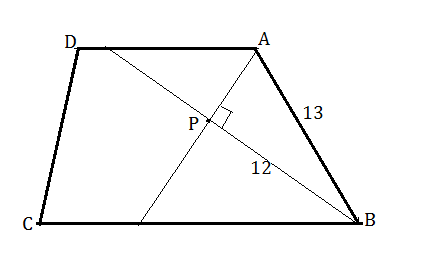
Сумма углов при боковой стороне трапеции равна 180°
Т.к. биссектрисы делят эти углы пополам, то сумма этих половин
∠АВР+∠ВАР=90°
Следовательно третий угол треугольника ВАР
∠ВРА=180°-90°=90°
и треугольник ВРА прямоугольный.
Отношение катета ВР к гипотенузе АВ указывает на принадлежность треугольника ВАР к "пифагоровым тройкам" и АР=5
Проверим по т.Пифагора:
АР=√(13²=12²)=
5