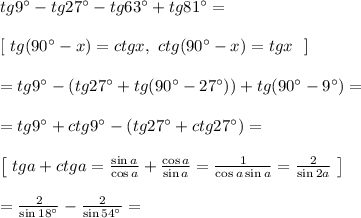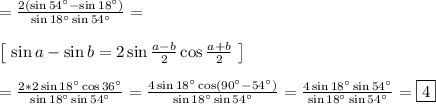tg9-tg27-tg63-tg81=4
[tg(90-x)=ctgx, ctg(90-x)=tgx]=tg9-(tg27+tg(90-27))+tg(90-9)-tg9+ctg9-(tg27+ctg27)=[tga+ctga=sina/cosa+cosa/sina=1/cosa*sina=2/sin2a]=2/sin18-2/sin54=2(sin54-sin18)/sin18*sin54=[sina-sinb=2sin*((a-b)/2)*cos((a+b)/2)=2*2sin18cos36/sin18sin54=4sin18cos(90-54)/sin18sin54=4sin18sin54/sin18sin54=4
все цифры в градусах, смотри, если так не понятно, фото прикрепляю