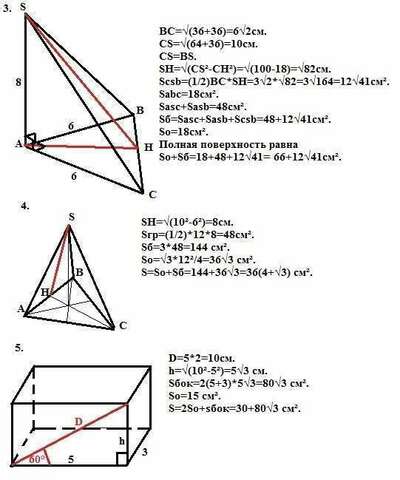
3. Основание пирамиды - прямоугольный треугольникАВС, а ее высота SA - перпендикуляр из вершины А. Тогда боковые грани ASB и ASC - прямоугольные треугольники. По Пифагору ВС=√(36+36)=6√2см.
СS=√(64+36)=10см.
CS=BS.
SH=√(CS²-CH²)=√(100-18)=√82см.
Scsb=(1/2)BC*SH=3√2*√82=3√164=12√41см².
Sabc=18см².
Sasc+Sasb=48см².
Sб=Sasc+Sasb+Scsb=48+12√41см².
So=18см².
Полная поверхность равна So+Sб=18+48+12√41=66+12√41см².
4. Апофема боковой грани равна по Пифагору √(10²-6²)=8см.
Площадь боковой грани по Пифагору равна Sгр=(1/2)*12*8=48см².
Площадь боковой поверхности равна Sб=3*48=144 см².
Площадь основания по формуле So=√3*а²/4 равна:
So=√3*12²/4=36√3 см².
Площадь полной поверхности пирамиды равна S=So+Sб=144+36√3=36(4+√3) см².
5. У прямоугольного параллелепипеда все грани - прямоугольники. Большая боковая рань параллелепипеда делится диагональю на два прямоугольных треугольника, в которых один из катетов (большая сторона основания параллелепипеда) лежит против угла 30° (так как второй острый угол равен 60° - дано). Значит диагональ большей грани параллелепипеда равна 5*2=10см, а высота параллелепипеда по Пифагору равна h=√(10²-5²)=5√3 см.
Площадь боковой поверхности параллелепипеда равна периметру основания, умноженному на высоту, то есть Sбок=2(5+3)*5√3=80√3 см².
Площадь основания (прямоугольника) равна произведению его сторон, то есть So=15 см².
Полная поверхность равна S=2So+sбок=30+80√3 см².