Начиная с третьей строчки, в вашем предполагаемом решении содержится ошибка, вы некорректно привели всё к общему знаменателю.
Так что продолжим, начиная с ещё правильной второй строки вашего рассуждения.
Но! Следует сделать важно замечание, которое имеет очень серьёзные последствия для всего решения.
Область определения заданной функции вовсе не вся числовая ось, а только положительные числа, поскольку на отрицательных числах функция логарифма в действительных числах не определена.
Итак  ;
;
Далее, продолжаем ваше решение:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
![x = -\frac{1}{ \sqrt[3]{3} } x = -\frac{1}{ \sqrt[3]{3} }](https://tex.z-dn.net/?f=+x+%3D+-%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B3%7D+%7D+) ;
;
Или сразу можно записать в интервальном виде:
![3x^3 + 1 = ( x + \frac{1}{ \sqrt[3]{3} } ) ( x^2 - \frac{x}{ \sqrt[3]{3} } + \frac{1}{ \sqrt[3]{9} } ) 3x^3 + 1 = ( x + \frac{1}{ \sqrt[3]{3} } ) ( x^2 - \frac{x}{ \sqrt[3]{3} } + \frac{1}{ \sqrt[3]{9} } )](https://tex.z-dn.net/?f=+3x%5E3+%2B+1+%3D+%28+x+%2B+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B3%7D+%7D+%29+%28+x%5E2+-+%5Cfrac%7Bx%7D%7B+%5Csqrt%5B3%5D%7B3%7D+%7D+%2B+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B9%7D+%7D+%29+) ;
;
![f'_x (x) = ( 1 + \frac{1}{ x \sqrt[3]{3} } ) ( x^2 - \frac{x}{ \sqrt[3]{3} } + \frac{1}{ \sqrt[3]{9} } ) f'_x (x) = ( 1 + \frac{1}{ x \sqrt[3]{3} } ) ( x^2 - \frac{x}{ \sqrt[3]{3} } + \frac{1}{ \sqrt[3]{9} } )](https://tex.z-dn.net/?f=+f%27_x+%28x%29+%3D+%28+1+%2B+%5Cfrac%7B1%7D%7B+x+%5Csqrt%5B3%5D%7B3%7D+%7D+%29+%28+x%5E2+-+%5Cfrac%7Bx%7D%7B+%5Csqrt%5B3%5D%7B3%7D+%7D+%2B+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B9%7D+%7D+%29+) ;
;
Причём, что следует и из предыдущего решения:
![D = \frac{1}{ \sqrt[3]{9} } - \frac{4}{ \sqrt[3]{9} } < 0 , D = \frac{1}{ \sqrt[3]{9} } - \frac{4}{ \sqrt[3]{9} } < 0 ,](https://tex.z-dn.net/?f=+D+%3D+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B9%7D+%7D+-+%5Cfrac%7B4%7D%7B+%5Csqrt%5B3%5D%7B9%7D+%7D+%3C+0+%2C+)
а значит, других корней нет. А поэтому, на области определения, т.е. при  0 " alt=" x>0 " align="absmiddle" class="latex-formula"> заданная функция всегда имеет положительную производную, а значит, всегда монотонно возрастает.
0 " alt=" x>0 " align="absmiddle" class="latex-formula"> заданная функция всегда имеет положительную производную, а значит, всегда монотонно возрастает.
О т в е т : интервал монотонного возрастания
функции  – это
– это 
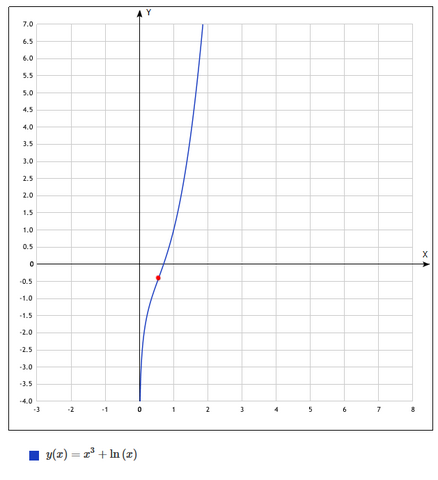
*** В дополнение о том, о чём автор не спрашивал. У данной функции есть два интервала разнонаправленного кручения (что видно и из графика). От ноля до некоторого значения она закручивается по часовой стрелки, а после некоторого числа – против. Для нахождения этой точки (точки перегиба) можно решить как уравнение относительно ноля, вторую производную заданной функции.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
![x = \frac{1}{ \sqrt[3]{6} } \approx 0.550 x = \frac{1}{ \sqrt[3]{6} } \approx 0.550](https://tex.z-dn.net/?f=+x+%3D+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B6%7D+%7D+%5Capprox+0.550+) ;
;
Это и есть абсцисса точки перегиба. Чтобы найти ординату точки перегиба, подставим это значение в исходную функцию:
![f( x=\frac{1}{ \sqrt[3]{6} } ) = ( \frac{1}{ \sqrt[3]{6} } } )^3 + \ln{ \frac{1}{ \sqrt[3]{6} } } = \frac{1}{6} - \frac{1}{3} \ln{6} = \frac{ 1 - 2 \ln{6} }{6} \approx -0.431 f( x=\frac{1}{ \sqrt[3]{6} } ) = ( \frac{1}{ \sqrt[3]{6} } } )^3 + \ln{ \frac{1}{ \sqrt[3]{6} } } = \frac{1}{6} - \frac{1}{3} \ln{6} = \frac{ 1 - 2 \ln{6} }{6} \approx -0.431](https://tex.z-dn.net/?f=+f%28+x%3D%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B6%7D+%7D+%29+%3D+%28+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B6%7D+%7D+%7D+%29%5E3+%2B+%5Cln%7B+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B6%7D+%7D+%7D+%3D+%5Cfrac%7B1%7D%7B6%7D+-+%5Cfrac%7B1%7D%7B3%7D+%5Cln%7B6%7D+%3D+%5Cfrac%7B+1+-+2+%5Cln%7B6%7D+%7D%7B6%7D+%5Capprox+-0.431+) ;
;
Поскольку это единственный корень, то, с учётом общей алгебраической положительности второй производной, она положительна после него и отрицательна до.
Таким образом, на ![x \in ( 0 ; \frac{1}{ \sqrt[3]{6} } ) x \in ( 0 ; \frac{1}{ \sqrt[3]{6} } )](https://tex.z-dn.net/?f=+x+%5Cin+%28+0+%3B+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B6%7D+%7D+%29+) и
и  – вторая производная отрицательна, т.е. график функции выпуклый, а кручение графика происходит по часовой стрелки.
– вторая производная отрицательна, т.е. график функции выпуклый, а кручение графика происходит по часовой стрелки.
На ![x \in ( \frac{1}{ \sqrt[3]{6} } ; +\infty ) x \in ( \frac{1}{ \sqrt[3]{6} } ; +\infty )](https://tex.z-dn.net/?f=+x+%5Cin+%28+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B6%7D+%7D+%3B+%2B%5Cinfty+%29+) и
и  – вторая производная положительна, т.е. график функции вогнутый, а кручение графика происходит против часовой стрелки.
– вторая производная положительна, т.е. график функции вогнутый, а кручение графика происходит против часовой стрелки.