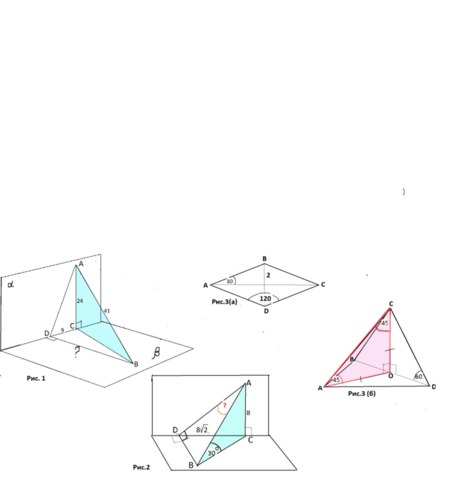
Задача 1.
Делаем рисунок 1.
Обратим внимание на то, что все фигуры - прямоугольные треугольники.
ВD найдем из треугольника ВСD, в котором ВD -катет, СВ - биссектриса.
Найдем эту биссектрису.
СВ²=АВ²-АС²=1681-576=1105
ВD²=СВ²-СD²=1105-81=1024
ВD=√1024=32 см
-------------------------------------------------
Задача 2
Делаем второй рисунок -Рис.2
Необходимо найти угол DАВ.
Для этого необходимо знать длину АD - катета прямоугольного треугольника АDВ, прилежащего к углу ВАD
Найдем AD из прямоугольного треугольника DCA по теореме Пифагора.
AD=√( DС²+АС²)=√(128+64)= 8√3 см
АВ=АС: sin(30°)=16 cм
cosDАВ=AD:АВ=8√3:16=√3:2 - Это косинус 30°
Угол DАВ=30°
----------------------------------------------------------------
Задача 3
Для того, чтобы ответить на вопрос задачи, нужно знать половину длины большей диагонали ромба.
Смотрим Рис.3(а)
Поскольку тупой угол ромба равен 120°,
острый его угол равен 60,
и диагональ BD делит ромб на два равносторонних треугольника,
отсюда сторона ромба равна 4 см
Необходимая нам половина длины диагонали ромба - это высота равностороннеготреугольника ABD и она равна
АО=(АВ√3):2=2√3 см
На втором рисунке к этой задаче (Рис. 3(б)
половины большей диагонали ромба образуют прямой угол АОС и
равнобедренный треугольник АОС с катетами, равными 2√3 см
АС из этого равнобедренного треугольника равна
АС=2√3*√2=2√6 см