13.
см. рисунок в приложении
О- точка пересечения АС и BD
Δ АОВ- равнобедренный ( диагонали АС и BD образуют со стороной АВ равные углы по условию, отмечены желтыми дугами)
Значит АО=ОВ
Треугольник АОD равен треугольнику ВОС
∠1=∠2 как вертикальные
∠OAD=∠OBC как разности равных углов (из равных углов DAB и CBA отнимаем равные, отмеченные желтым)
АО=ОВ
из равенства треугольников ОD=OC
AC=AO+OC=BO+OD=BD
14
∠3=∠4 по условию треугольники равны, значит и углы равны
АС=А₁С₁ из равенства треугольников и стороны равны
∠1=∠2 так как ∠С=∠С₁ и из равных углов вычли равные
Треугольники АСD и A₁C₁D₁ равны по стороне и двум прилежащим к ней углам
из равенства треугольников следует равенство сторон:
AD=A₁D₁
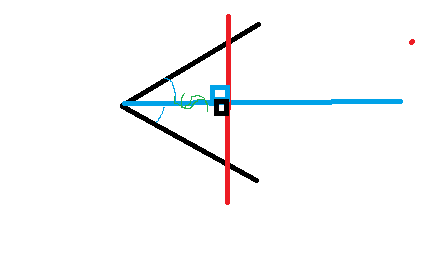
15. см. рисунок
Прямоугольные треугольники равны по катету (общий отрезок) и острому углу.
Из равенства треугольников следует равенство сторон