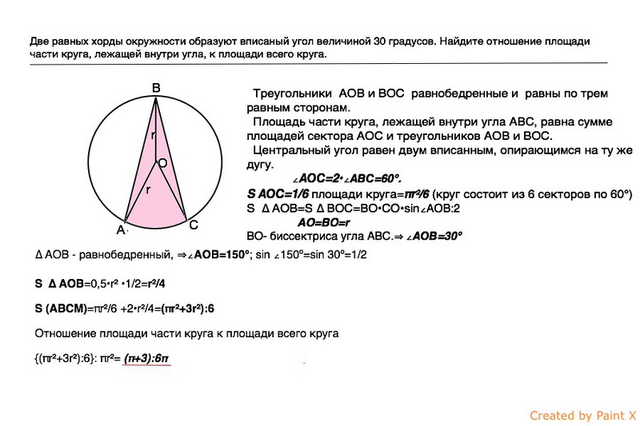
Две равных хорды окружности образуют вписанный угол величиной 30 градусов. Найдите отношение площади части круга, лежащей внутри угла, к площади всего круга.
-----------
Обозначим центр круга О, хорды - АВ и ВС.
Угол АВС=30°
Соединим концы хорд с центром О.
Треугольники АОВ и ВОС равнобедренные и равны по трем равным сторонам.
Площадь части круга, лежащей внутри угла АВС, равна сумме площадей сектора АОС и треугольников АОВ и ВОС.
Центральный угол равен двум вписанным, опирающимся на ту же дугу.
∠АОС=2•∠АВС=60°.
S АОС=1/6 площади круга= πr²/6 (т.к. градусная мера сектора равна 1/6 градусной меры полного круга)
S ∆ AOB=S ∆ ВОС=ВО•CO•sin∠AOB:2
AO=BO=r
ВО- биссектриса угла АВС.⇒
∠АОВ=30°
∆ АОВ - равнобедренный, ⇒∠АОВ=150°; sin ∠150º=sin 30º=1/2
S ∆ AOB=0,5•r² •1/2=r²/4
S (ABCM)=πr²/6 +2•r²/4=(πr²+3r²):6
Отношение площади части круга к площади всего круга
{(πr²+3r²):6}: πr²= (π+3):6π