ПОМОГИТЕ!!!!!!!!!!!!! ** плоскости альфа дан угол 60. точка М удалена от каждой стороны...

Question

ПОМОГИТЕ!!!!!!!!!!!!!
на плоскости альфа дан угол 60. точка М удалена от каждой стороны угла на 7, а от плоскости на 5. найдите расстояние от точки М до вершины угла
если не сложно, то с рисунком)

Answer 1

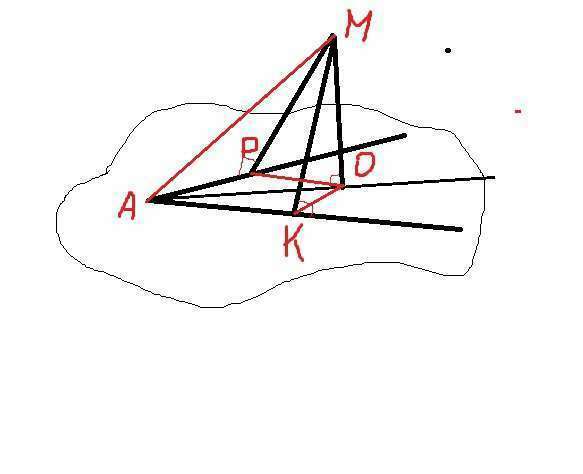
МО=5, МР=МК=7, ∠А=60°.
МК⊥АК⇒КО⊥АК.
КО = √(МК²-МО²)=√24.
∠ОАК=30⇒АК=ОК/(tg30°)=3√8/
 АМ ищем по теореме Пифагора для треугольника АМК, АМ=√(АК²+МК²)=√(72+49)=11. Вот, примерно так. Там еще нужно доказать равенство треуг. МРО и МКО и т, что АО - биссектриса угла А.

---

Comments

спасибо