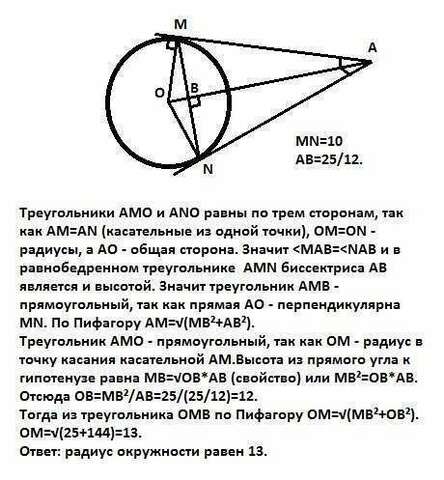
Треугольники АМО и АNО равны по трем сторонам, так как АМ=АN (касательные из одной точки), ОМ=ОN -радиусы, а АО - общая сторона. Значит Треугольник АМО - прямоугольный, так как ОМ - радиус в точку касания касательной АМ.Высота из прямого угла к гипотенузе равна МВ=√ОВ*АВ (свойство) или МВ²=ОВ*АВ.
Отсюда ОВ=МВ²/АВ=25/(25/12)=12.
Тогда из треугольника ОМВ по Пифагору ОМ=√(МВ²+ОВ²).
ОМ=√(25+144)=13.
Ответ: радиус окружности равен 13.