Так как в условии путаница с обозначениями, примем это условие так:
"В
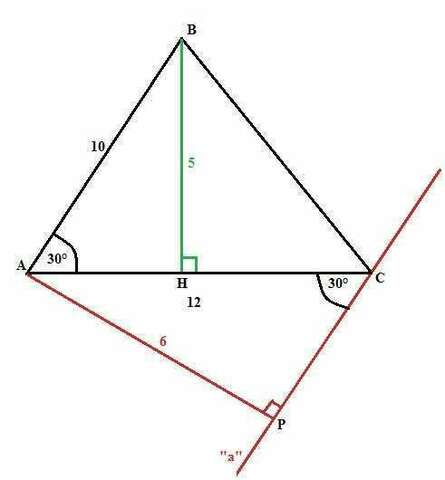
треугольнике АВС , угол А=30°. Сторона АС=12 см, АВ = 10 см, Через
вершину С проведена прямая "а", параллельная АВ. Найти :
а) расстояние от В
до АС ; б) расстояние между прямыми "а" и АВ".
Решение.
а) Расстояние от В до АС - это перпендикуляр ВН, опущенный из вершины В на сторону АС, то есть высота ВН треугольника АВС.
Так как угол А=30°, то эта высота - катет, лежащий против угла 30° и равен половине гипотенузы АВ, равной 10см.
Ответ: расстояние от В
до АС равно 5см.
б) Расстояние между прямыми "а" и АВ - это перпендикуляр, опущенный из любой точки прямой АВ на прямую "а", параллельную прямой АВ.
Опустим перпендикуляр АР на прямую "а". Полуяили прямоугольный треугольник АРС,
в котором угол <АСР=30°, так как <A=<ACP как внутренние накрест лежащие при параллельных "а" и АВ и секущей АС.<br>Тогда в треугольнике АСР катет АР лежит против угла 30° и равен половине гипотенузы АС, то есть АР=6см.
Ответ: расстояние между прямыми "а" и АВ равно 6см.