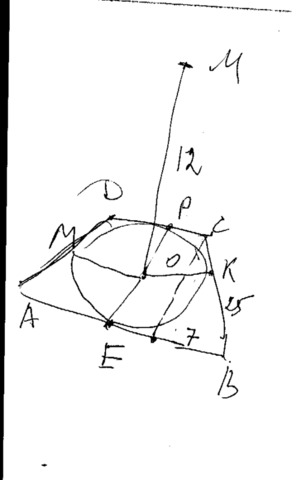
Если точка М одинаково удалена от сторон трапеции, то и основание перпендикуляра О, проведенного из М к плоскости трапеции одинаково удалено от сторон трапеции. О - центр окружности, вписанной в трапецию. МО⊥пл АВСD. В описанной трапеции суммы оснований и боковых сторон равны. Сумма оснований 18+32=50. Значит боковые стороны равны по 25. Высота трапеции равна диаметру окружности. Находим высоту.h =√(25²-7²) = 24. Радиус равен 12.
МО²=МР²-ОМ². МО=√0=0. Значит точка М лежит в плоскости. Что-то в условии неверно.