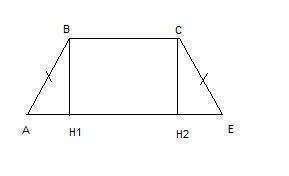
Построим высоты ВН1 и СН2. Отрезок Н1Н2, лежащий на основании АЕ, будет равен ВС.
Поскольку трапеция равнобедренная, то АН1=ЕН2. Найдем, чему равны эти отрезки:
АН1+Н1Н2+ЕН2=АЕ, но Н1Н2=ВС. Тогда
АН1+ВС+ЕН2=АЕ,
АН1+ЕН2=АЕ-ВС.
Поскольку АН1=ЕН2, выражение АН1+ЕН2=АЕ-ВС можно записать так:
АН1+АН1=АЕ-ВС
2АН1=АЕ-ВС
АН1=(АЕ-ВС):2, ЕН2=(АЕ-ВС):2
Найдем отрезок ЕН1:
ЕН1=Н1Н2+ЕН2=ВС+(АЕ-ВС):2
ЕН1=(ВС+АЕ):2