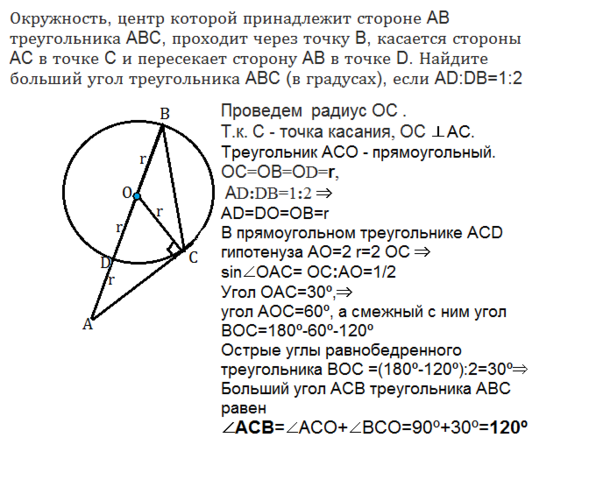
Окружность, центр которой принадлежит стороне AB треугольника ABC, проходит через точку B, касается стороны AC в точке C и пересекает сторону AB в точке D. Найдите больший угол треугольника ABC (в градусах), если AD:DB=1:2
-----------
Центр окружности лежит на АВ, следовательно, АD- диаметр.
Проведем радиус ОС .
Т.к. С - точка касания, ОС ⊥ АС.
Треугольник АОС - прямоугольный.
ОС=ОВ=ОD=r, АD:DB=1:2 ⇒
AD=DO=OB=r
В прямоугольном треугольнике АСD гипотенуза
AO=2 r=2 OC ⇒
sin∠OАС= OС:АО=1/2 ⇒
Угол ОАС=30º,⇒
угол АОС=60º, а смежный с ним угол ВОС=180º-60º-120º
Острые углы равнобедренного треугольника ВОС равны (180º-120º)
:2=30º⇒
Больший угол АСВ треугольника АВС равен
∠АСВ=∠АСО+∠ВСО=90º+30º=
120º