Ну, смотрите.
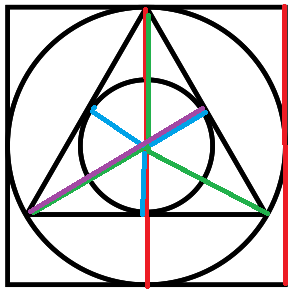
Сразу определимся, что нам надо найти. Площадь круга равна πr², значит, найти нужно радиус меньшего круга (на рисунке обозначен голубым цветом).
Диаметр окружности, вписанной в квадрат, равен его стороне (по рисунку это хорошо видно (красная линия в центре), значит, радиус окружности равен половине стороны квадрата и равен 12/2=6 см.
Радиус окружности, вписанной в квадрат, обозначен зеленым цветом. Поскольку треугольник правильный, то центр и вписанной в него, и описанной около него окружностей совпадает с точкой пересечения его биссектрис, высот, и, главное, медиан (нам в данном случае интересны именно медианы).
По теореме точка пересечения медиан треугольника делит каждую медиану в отношении 2:1 считая от вершины, то есть то, что на рисунке обозначено зеленым цветом, и есть 2 части от каждой медианы. Получается, что 2/3 медианы равны 6 см, откуда одна 1/3 равна 3 см, а вся медиана (на рисунке фиолетовый цвет) равна 3 см*3 части=9 см.
Из рисунка также видно, что радиус искомого круга (голубой цвет) равен как раз 1/3 медианы и равен соответственно 9/3=3 см.
Отсюда находим площадь меньшего круга по формуле πr²=3,14*(3 см)²=9*3,14=28,26 см². Но нам нужно (по заданию) найти ответ с точностью до десятых, т.е. округлить до десятых. Цифра после 2 десятых больше 5, следовательно, округляем в бОльшую сторону: 28,26 ≈ 28,3 см².
ОТВЕТ: S меньшего круга ≈ 28,3 см².