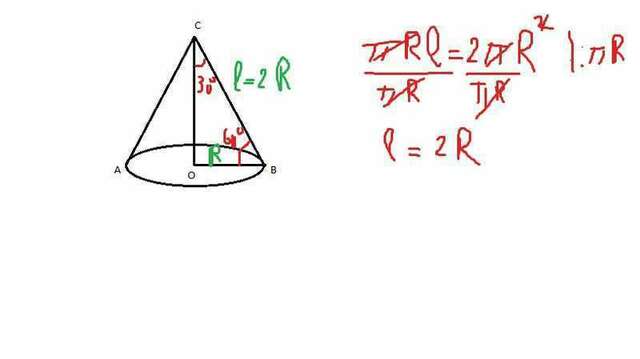Угол между образующей конуса и плоскостью основания равен углу между образующей и радиусом основания, проведенного к данной образующей. Площадь боковой поверхности конуса: pi*R*l, площадь основания - pi*R^2. Поскольку площадь боковой поверхности в два раза больше площади основания, то pi*R*l = 2*pi*R^2. упрощаем уравнение: l = 2R. Из рисунка CB = 2OB. Из прямоугольного треугольника COB: угол, который лежит против катета, который в два раза меньше гипотенузы, равен 30 градусов. OB - катет, CB - гипотенуза, следовательно, угол BOC = 30 градусов. Искомый угол CBO = 90 - 30 = 60 градусов.