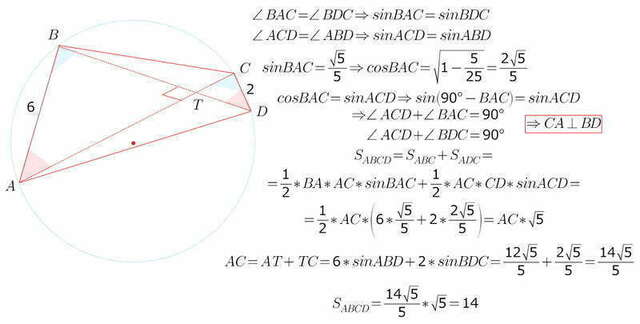
Хорошая задача)) из серии "как нетрудно догадаться..."
если увидеть, что диагонали этого 4-угольника перпендикулярны,
то дальше решение понятное... но вот как это "увидеть"...
очевидно, что раз речь о вписанном 4-угольнике, то
нужно искать равные (опирающиеся на равные дуги) углы...
и окажется, что даны синусы углов из одного треугольника)))
по теореме синусов получится соотношение: АТ = 2*ВТ и TD = 2*TC
и попытка записать косинус одного из данных углов (для теоремы косинусов) с целью найти еще одну сторону треугольника, привела (к вроде бы не очень очевидному)) решению...
известно: если А и В --острые углы прямоугольного треугольника,
т.е. ∠А + ∠В = 90°, то
sinA = cosB и cosA = sinB
площадь 4-угольника, у которого диагонали взаимно перпендикулярны,
можно еще вычислить как:
половина произведения его диагоналей)))
если найти BD = 10√5 / 5
S = AC*BD / 2