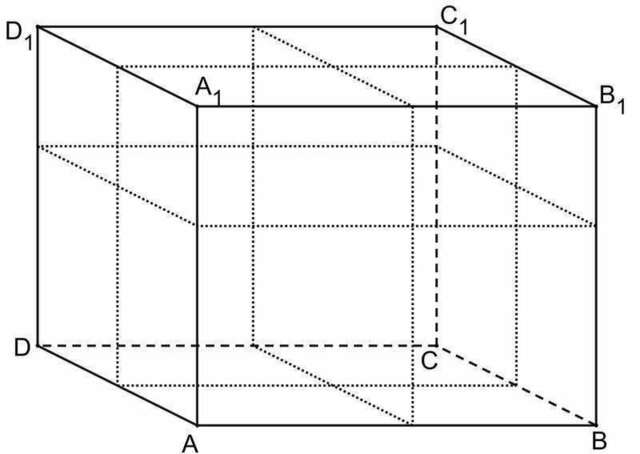
Деревянный брусок, имеющий форму прямоугольного параллелепипеда ABCDA_1B_1C_1D_1, распилили тремя распилами, параллельными граням, на 8 маленьких брусков (см. рисунок). Чему равна площадь поверхности бруска с вершиной C, если площадь поверхности бруска с вершиной A составляет 130, с вершиной B — 184, D — 220, A_1 — 210, B_1 — 288, C_1 — 448, D_1 — 340? (Если ответ не целый, в поле ответов следует записывать его в виде десятичной дроби, отделяя целую часть от дробной части точкой.)