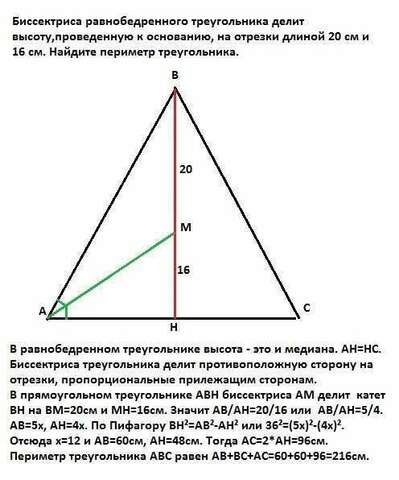
В равнобедренном треугольнике высота - это и медиана. АН=НС. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам. В прямоугольном треугольнике АВН биссектриса АМ делит катет ВН на ВМ=20см и МН=16см. Значит АВ/АН=20/16 или АВ/АН=5/4. АВ=5х, АН=4х. По Пифагору ВН²=АВ²-АН² или 36²=(5х)²-(4х)². Отсюда х=12 и АВ=60см, АН=48см. Тогда АС=2*АН=96см. Периметр треугольника АВС равен АВ+ВС+АС=60+60+96=216см.
Ответ: 216см.