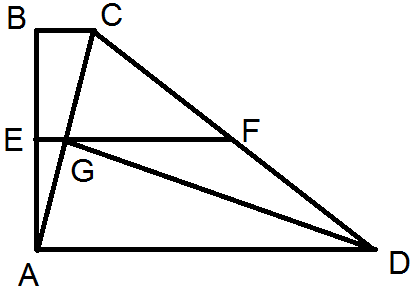
BCA = CAD = ACD
треугольник ACD - равносторонний и CD = AD
EF - средняя линия и делит AC пополам, т.е. AG = GC
BC + AD = 13.5 * 2 = 27
BC = AC * cos BCA = 12 * cos BCA
AD = 27 - BC = 27 - 12 * cos BCA
AG = 12 / 2 = 6 = AD * cos CAD = (27 - 12 * cos BCA) * cos BCA
Обозначим cos BCA = t, тогда
6 = (27 - 12t) t
12t^2 - 27t + 6 = 0
(t - 2)(12t - 3) = 0
12t - 3 = 0 (косинус не может равняться 2 и поэтому (t-2)<>0 )
t = 0.25
BC = 12t = 3
AD = CD = 27-BC = 24
BA =  =
=