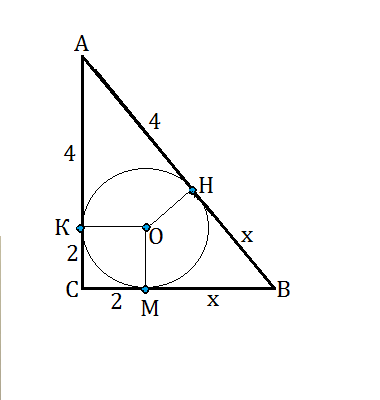В прямоугольном треугольнике вписана окружность радиусом 2 см так, что один из...

Question

В прямоугольном треугольнике вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4см. Найти гипотенузу прямоугольного треугольника.

Answer 1

Пусть дан треугольник АВС и вписанная в него окружность с центром О.  
К - точка касания на АС,  
М - точка касания на ВС, 
Н - точка касания на АВ. 
КС=СМ=r=2 
АК=4 
Отрезки касательных к окружности, проведенных из одной точки, равны. ⇒ 
АН=АК=4 
МВ=ВН=х 
По т.Пифагора  
АВ²=АС²+ВС²  
(4+х)²=6²+(2+х)²⇒ 
4х=14 
ВН=х=3,5 ⇒ 
АВ=АН+ВН=7,5 см

---