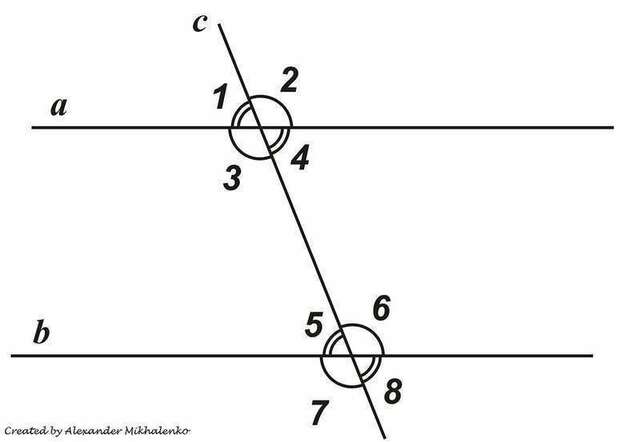
Пусть параллельные прямые a и bпересечены секущей MN (c). Докажем что накрест лежащие углы 3 и 6 равны. Допустим, что углы 3 и 6 не равны. Отложим от луча MN угол PMN, равный углу 6, так, чтобы угол PMN и угол 6 были накрест лежащими углами при пересечении прямых МР и b секущей MN. По построению эти накрест лежащие углы равны, поэтому МР||b. Мы выяснили, что через точку М проходят две прямые (прямые a и МР), параллельные прямой b. Но это противоречит аксиоме параллельных прямых. Значит, наше допущение неверно и угол 3 равен углу 6.