Основание наклонной треугольной призмы авса1в1с1 -- прямоугольный треугольник ывс, у...

Question

Основание наклонной треугольной призмы авса1в1с1 -- прямоугольный треугольник ывс, у которого ав=12, вс=16, угол авс =90 градусов. Боковая граньаа1с1с является квадратом. Вычислите объём призмы, если известно, что боковые ребра пирамиды в1авс равны.

Answer 1

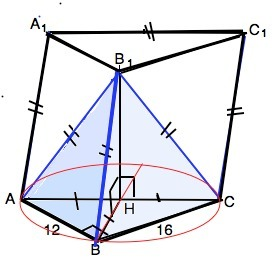
Грань АА1С1С - квадрат. 

АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.

По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒

Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы. 

∆ АВС прямоугольный, R=АС/2=10. 

АН=СН=ВН=10. 

Высота призмы совпадает с высотой В1Н пирамиды.

По т.Пифагора 

В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3

Формула объёма призмы

 V=S•h где S - площадь основания, h - высота призмы. 

S-12•16:2=96 (ед. площади)

V=96•10√3=960√3 ед. объёма.

---