** сторонах AB и BC треугольника ABC отмечены точки P и Q так, что углы BPC и BQA равны,...

Question

На сторонах AB и BC треугольника ABC отмечены точки P и Q так, что углы BPC и BQA равны, BP=BQ, AB=20, BQ=12, CP=11. Найдите периметр треугольника COQ, где O — точка пересечения прямых AQ и CP.

Answer 1

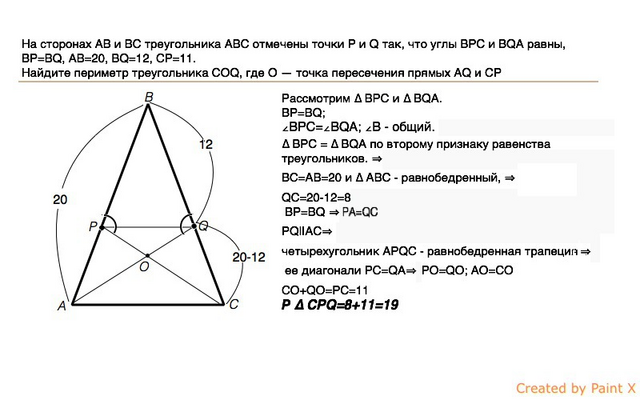
На сторонах AB и BC треугольника ABC отмечены точки P и Q так, что углы BPC и BQA равны, BP=BQ, AB=20, BQ=12, CP=11. 

Найдите периметр треугольника COQ, где O — точка пересечения прямых AQ и CP

––––––––––––––

Рассмотрим ∆ ВРС и ∆ BQA.

BP=BQ;  

∠BPC=∠BQA; ∠В - общий. 

∆ ВРС = ∆ BQA по второму признаку равенства треугольников. ⇒

ВС=АВ=20 и ∆ АВС - равнобедренный, ⇒ 

QC=20-12=8

 BP=BQ ⇒PA=QC ⇒ 

PQ||AC⇒ 

четырехугольник APQC - равнобедренная трапеция, и ее диагонали PC=QA и тогда

PO=QO; AO=CO

CO+QO=PC=11

Р ∆ CPQ=8+11=19 (ед. длины)

---