1.
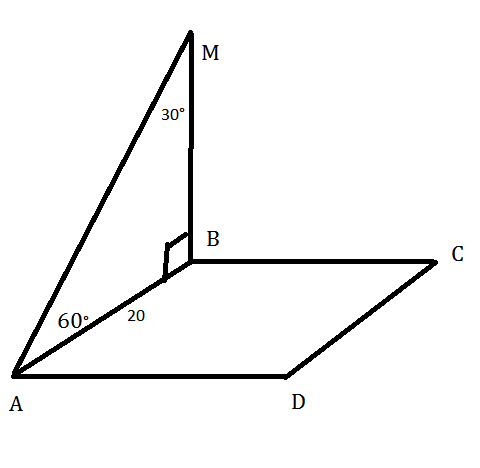
MB⊥пл. АВСD, значит МВ перпендикулярна любой прямой, лежащей в плоскости ABCD, в том числе и АВ.
∠МВА=90°
Из прямоугольного треугольника АМВ
МВ=АВ·tg60°=20√3
2.
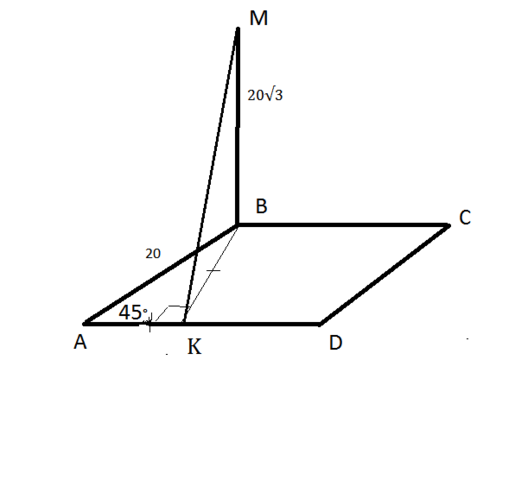
Плоскости MAD и ADВ пересекаются по прямой AD
(поэтому двугранный угол обозначен так: М - точка первой плоскости, AD - общая прямая, В - точка второй плоскости, получилось МADВ)
Чтобы построить линейный угол двугранного угла проводим ВК⊥AD.
MB⊥BК ( см. доказательство в п.1)
По теореме о трех перпендикулярах МК⊥AD.
∠МКВ- линейный угол двугранного угла MADB.
ΔАВК- прямоугольный равнобедренный ( по условию ∠А=45°),
значит АК=ВК=20·sin 45°=10√2
tg∠MKB=MB/BK=20√3/10√2=√6
∠MKB=arctg √6