В равнобедренном треугольнике АВС АВ=ВС=а, угол В = альфа. Расстояние от точки М до...

Question

46 просмотров

В равнобедренном треугольнике АВС АВ=ВС=а, угол В = альфа. Расстояние от точки М до плоскости треугольника также равно а. Проекцией точки М на плоскость треугольника является точка М1 пересечения медиан треугольника АВС. Найдите расстояния от точки М до вершин треугольника и до прямых, содержащих его стороны.

Геометрия ABC1234567_zn (2.9k баллов) 10 Март, 18 | 46 просмотров

Дан 1 ответ

Правильный ответ

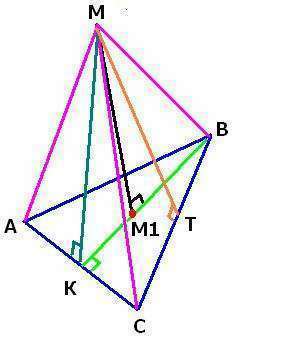
Начнем с того, что ребра МВ МС МА равны ( т.к. М1С=М1А=М1В - радиусы описанной окружности и высота ММ1 для них общая и составляет с ними угол в 90). Значит достаточно найти только одно ребро.

Высота в р/б треуг АВС ВК - она же и биссектриса и медиана. т. М - точка пересечения медиан, тогда ВМ1=2/3*ВК, а М1К=ВК/3.

Угол КВС=углу КВА (ВК - биссектр), тогда угол КВС=углу КВА=альфа/2=0.5А

Поэтому cos 0.5А=ВК/ВС, тогда ВК=cos 0.5А*ВС=а*cos 0.5А, тогда

М1К=(а*cos 0.5А)/3

M1B=2*(а*cos 0.5А)/3

найдем МК по т. Пиф:

$MK^2=M1M^2+M1K^2\\ \\MK^2=a^2+\frac{a^2cos^20.5A}{9}\\ \\MK^2=\frac{9a^2+a^2cos^20.5A}{9}\\ \\MK^2=\frac{a^2(9+cos^20.5A)}{9}\\ \\MK=\frac{a\sqrt{(9+cos^20.5A)}}{3}$

найдем МB по т. Пиф:

$MB^2=M1M^2+M1B^2\\ \\MB^2=a^2+\frac{4a^2cos^20.5A}{9}\\ \\MB^2=\frac{4a^2*(2.25+cos^20.5A)}{9}\\ \\MB=\frac{2a\sqrt{(2.25+cos^20.5A)}}{3}$

Т.к. МВ=МС, то МТ - высота, медиана и биссектриса, тогда

ТС=ТВ=а/2

Найдем МТ по т Пиф:

$MT^2=MB^2-TB^2$

$MT^2=a^2+\frac{4a^2cos^20.5A}{9}-\frac{a^2}{4}\\ \\MT^2=\frac{4a^2}{4}+\frac{4a^2cos^20.5A}{9}-\frac{a^2}{4}\\ \\MT^2=\frac{3a^2}{4}+\frac{4a^2cos^20.5A}{9}\\ \\MT^2=\frac{27a^2+16a^2cos^20.5A}{36}\\ \\MT^2=\frac{a^2(27+16cos^20.5A)}{36}\\ \\MT=\frac{a\sqrt{(27+16cos^20.5A)}}{6}$

NY444_zn (45.8k баллов) 10 Март, 18