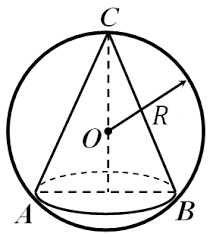
Найдем длину окружности основания конуса:
Lкон.=пD=3,14х9 (9 так как осевое сечение правильный треуг. со стороной 9)
Теперь найдем радиус сферы:
для правильного треугольника АВС вписанного в окружность Rокр.=√3/3 а (где а - сторона треугольника).
Теперь находим длину окружности сферы:
Lсф.=2пR=2х3,14х9х√3/3=6х3,14х√3
Lсф./Lкон.=(6х3,14х√3)/3,14х9=2√3/3=2/√3