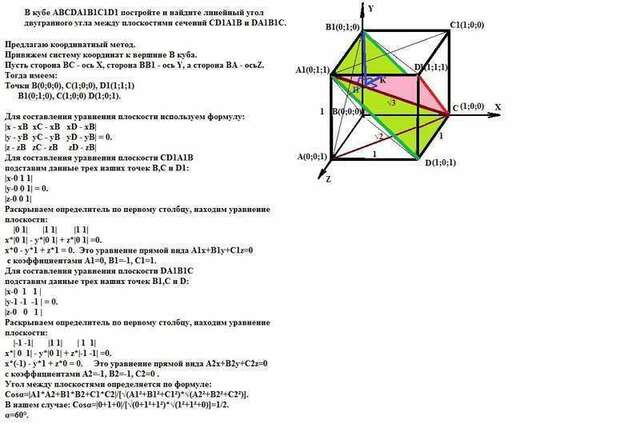
Предлагаю координатный метод.
Привяжем систему координат к вершине В куба.
Пусть сторона ВС - ось Х, сторона ВВ1 - ось Y, а сторона ВА - осьZ.
Тогда имеем:
Точки В(0;0;0), C(1;0;0), D1(1;1;1)
B1(0;1;0), C(1;0;0) D(1;0;1).
Для составления уравнения плоскости используем формулу:
|x - xB xC - xB xD - xB|
|y - yB yC - yB yD - yB| = 0.
|z - zB zC - zB zD - zB|
Для составления уравнения плоскости CD1A1B
подставим данные трех наших точек B,C и D1:
|х-0 1 1|
|y-0 0 1| = 0.
|z-0 0 1|
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
|0 1| |1 1| |1 1|
х*|0 1| - y*|0 1| + z*|0 1| =0.
x*(0-0) - y*(1-0) + z*(1-0) = 0. Или
х*(0)-y*(-1)+z*(1)=0 Это уравнение прямой вида А1х+В1y+C1z=0 с коэффициентами А1=0, В1=-1, С1=1.
Для составления уравнения плоскости DA1B1С
подставим данные трех наших точек B1,C и D:
|х-0 1 1 |
|y-1 -1 -1 | = 0.
|z-0 0 1 |
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
|-1 -1| |1 1| | 1 1|
х*| 0 1| - y*|0 1| + z*|-1 -1| =0.
x*(-1-0)) - y*(1-0) + z*(-1+1) = 0. Или
х*(-1)-y*(1)+z*(0)=0 Это уравнение прямой вида А2х+В2y+C2z=0 с коэффициентами А2=-1, В2=-1, С2=0 .
Угол между плоскостями определяется по формуле:
Cosα=|A1*A2+B1*B2+C1*C2|/[√(A1²+B1²+C1²)*√(A2²+B2²+C2²)].
В нашем случае: Cosα=|0+1+0|/[√(0+1²+1²)*√(1²+1²+0)]=1/2.
α=60°.
Ответ: искомый угол равен 60°.