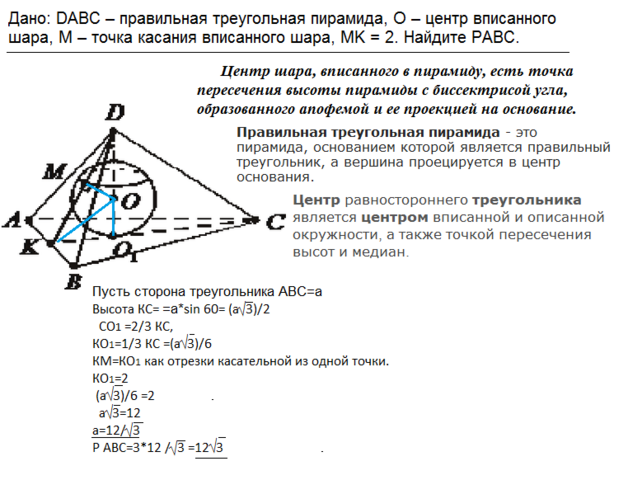
Дано: DABC – правильная треугольная пирамида, O – центр вписанного шара, M – точка касания вписанного шара, MK = 2. Найдите PABC
----
Вспомним несколько определений: Правильная треугольная пирамида - это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.
Центром равностороннего треугольника является точка пересечения биссектрис, высот и медиан.
Центр шара, вписанного в пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание.
Решение.
Пусть сторона ∆ АВС=а
Тогда высота КС=а*sin 60º
KC=a√3):2
КО₁=КС:3=a√3)
:6
КО₁=КМ=2 как отрезки касательных из одной точки. ⇒
a√3)
:6=2
a=12/√3
Р=3*12/√3
Р=12√3