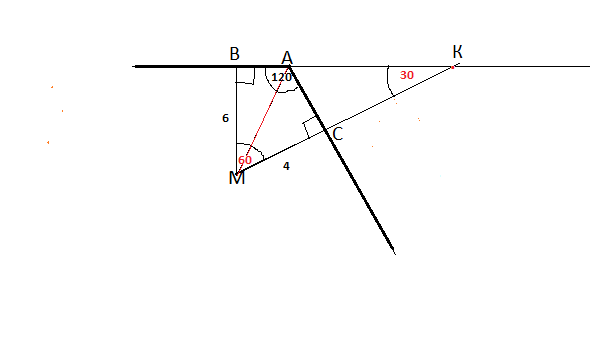
Точка М лежит внутри двугранного угла величиной 120 градусов и удалена от его граней на расстояния соответственно 4 и 6. Найдите расстояние от М до ребра двугранного угла.
Опишу подробно.
Рисуем данный угол 120° как бы в разрезе, т.е. вид сверху.
Обозначим вершину данного угла А.
В нутри угла отмечаем точку М.
Расстояние от точки до плоскости - перпендикуляр.
Опустим из М перпендикуляры к сторонам угла.
Обозначим точку пересечения со стороной угла более длинного отрезка, равного 6, - В , более короткого, равного 4, - С.
Т.к. сумма углов четырехугольника 360°, углы В и С прямые по построению, то
угол ВМС=180°-120°=60°.
Продлим сторону ВА и построим смежный с углом А угол.
Он, как смежный, равен 180°-120°=60°
Продлим МС до пересечения с ВА, обозначим точку пересечения К.
Получился прямоугольный треугольник ВМК.
В нем
угол ВМК равен 60° . угол ВКМ=30°
МК=ВМ:sin( 30°)=12
СК=МК-МС=12-4=8
АС=CК:Ctg (30°)=8:√3
Из прямоугольного треугольника АМС по теореме Пифагора найдем МА.
МА²=АС²+МС²=(8:√3)²+4²=64/3+16=112/3
МА=√(112/3)=4√(7/3)